R1年電験3種理論問2解説~コンデンサ~
こんにちは。イルカです。
今回はR1年理論の第2問を解説しました。以下の動画になります。
コンデンサの問題
コンデンサに関する基本的な問題かと思います。公式を把握していれば問題なく解くことができます。
回路が肝となるのは当然ですが、問題文のなかでは極板の面積が同一であることが重要です。また、導出する電界の強さの単位も確認しておきましょう。
コンデンサの知識は電気の理解には欠かせない知識であり、回路の問題でも活きてきます。
ポイントが多くて大変かもしれませんが、性質を理解し、解けるように繰り返し学習しましょう。
問題のポイント:コンデンサの式と電界
Q=CV、V=Ed、C=εS/d を使いこなそう!
というわけで式は覚えたほうが良いです。
ちなみに、よく「公式を覚える」というフレーズで勘違いしている人が多いのですが、使い方まで理解して初めて「公式を覚えた」ことになります。余談ですね、すみません。
静電容量
静電容量は電荷のためやすさを表します。
面積が広いほどためやすい、また極板間距離は短いほど電極間の引きつけが強くなり、たまりやすそう、と感覚的にわかるので分母分子どっちだっけってなったときも感覚で思い出せるでしょう。
電界
電界は、電位の傾きを表します。こちらの式も覚えている方は多いかと思います。極板間は直線電界であり、電位V、距離dなのでこのような式になるのはわかりますね。ちょっと考えれば分かる式なので、意識して覚えようとしなくても自然と身につくかと思います。
ちなみに厳密に言うと、極板端は直線電界ではないのですが、基本的には無視かまいません。問題文にもそうした記載はあります。
また、ガウスの法則を各極板に適用してみましょう。各極板から生じる電界Es(添字はシングルのs、作っている途中の適当な思いつきでつけたので一般的ではありません)が求められます。極板間の電界は両極板の電界和というわけです。
ちなみに、このアプローチが思いつかなかったとしても、覚えているであろうポイントに記載の式からもこのように導出可能です。もちろんこの性質を知っているというだけでも十分でしょう。(相変わらず雑な資料ですみません)

回路を整理する
問題の回路を見てみると、並列回路になっていますね。回路の問題のたびに言っているのですが、回路は整理することが肝だと思っています。並列回路では、いくら回路がならんでいようと各分岐の電圧は同じです。そうなると、一番右の回路の有無は、解答する電界とは何ら関係がないので省略してしまって構いません。
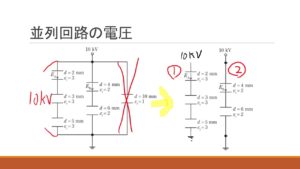
すると、それぞれ直列回路になります。これらをひとつづつ考えていきましょう。各コンデンサは比誘電率も極板面積も同じなので、簡単に一つのコンデンサとすることができますね。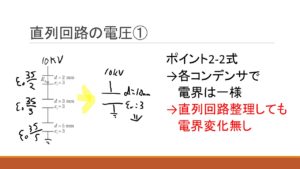
ちなみに誘電率には触れていませんでしたが、ε0は真空での誘電率で定数であり、誘電率は比誘電率εrに比例します。
というわけで、簡単になったコンデンサの電界を、ポイント記載の式で求めてやれば解答がでてきます。
ちなみに、コンデンサをまとめなくとも、各コンデンサの静電容量を導出、それぞれの分圧から地道な計算で電界を導出することができます。
今回は記載しませんが、計算練習として試してみても良いでしょう。
まとめ
コンデンサの問題は頻出ですが、覚えておく式はポイント記載の3つ。使いこなすことができれば基本的には解けない問題はないはずです。コンデンサの問題に限らず、複雑な問題が出題された場合は、まずは、与えられた状況を整理してみるのが良いと思います。
修正点や意見、アドバイス等ございましたらツイッター等で連絡いただければと思います。
余談
ブログで数式を入力するのは手間なのでところどころyoutubeの画像を貼り付けているのですが見づらいでしょうか・・・?
なんとなく理論の動画ばかり作成していたのですが、自分の勉強も兼ねて苦手な法規を勉強しながら解説していくのもありかなぁと思っています。



コメント