電験三種、H29年度理論問2の解説動画を紹介します。
今回も、以前投稿した動画について文字で補足しつつ説明します。
例のごとく雑な絵ですみません。
問題の概要
コンデンサの充電時の特性や回路の構成に関する問題です。
並列接続の前後の状態を書き出す必要があります。
コンデンサに関する公式を幅広く知っている必要があり、
練習用としては良い問題です。
逆に本番では、問題文が長く、状況もやや複雑面倒なので、
後回しにして最後に時間があれば解くという方針が良いでしょう。
ポイント:コンデンサの特性
・電荷の式:Q=CV
・静電容量の式:C=ϵS/d
・電界の式:E(r)=V/d
面積が広いほど、間隔が狭いほど電荷は溜まりやすくなります。
また、電界は電位の傾きです。極板間は、直線電界となりますので、
単純に電位差を距離で割ってあげれば電界が求められます。
直感的にもわかるため、式は思い出せるでしょう。
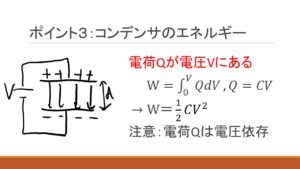
ポイント:コンデンサのエネルギー
電荷Qを電圧Vまでもってくるために必要なエネルギーということで、
電荷を電圧で積分することにより導出が可能になります。
ただ、この式はよく使うので覚えてしまっても良いと思います。
ど忘れしたら導出できるということは知っておきましょう。
並列前の状態
まずは、並列前の状態です。
問題文には「電界が等しくなるように充電」とあります。
コンデンサCのみ、極板間距離が2倍なので、
電界を同じにするために2倍の電圧をかけることになります。
それぞれ、接続する前のエネルギーが求められます。
問題:並列後の状態
並列後は、このような回路になりますね。
コンデンサA,B,Cの並列回路ということです。
コンデンサの並列回路において、コンデンサの静電容量は、
並列につながる各コンデンサの静電容量の和となります。
また、電源から切り離して並列した場合、
コンデンサの電荷は並列回路の外に逃げられないので、
電荷の合計量は並列前後で変わりません。
これらを踏まえますと、各コンデンサにかかる電圧も求められますね。
必要な要素が揃えば、計算して並列接続後のエネルギーが求められます。
並列前後の比較
並列前後のエネルギーについて分かりましたのでこれらを比較します。
あとは計算するだけですね。
並列前と並列後の比率は、計算すると、0.9になり、(2)が正解です。
まとめ
今回の問題は、やや時間がかかる複雑な問題でした。
ただ、複雑な問題で、どうしていいかわからなくなってしまったときは、
ポイントとなる式から、コンデンサの状況を一つ一つ書き出していくと、
なんとなくやるべきことがみえてくるとおもいます。
コンデンサの問題に限らず、複雑な問題が出題された場合は、
まずは、基本的な知識から与えられた状況を整理してみるのが良いです。
電験本番では、このような複雑な問題は避けたほうが良いかもしれません。
時間に余裕がある場合は、今いったような方法で取り掛かってみましょう。
電験の演習としては、要点が詰め込まれており、良い問題です。
今回、ポイントとして説明した式は、
コンデンサの回路問題では使用頻度が高いので
ぜひとも理解しておいてください。



コメント